机器人手眼标定流程详解：相机标定在机器人视觉中的重要性及应用

在机器人技术领域，坐标转换与标定扮演着核心角色。研究重点在于不同坐标系间的转换技巧和标定方法。这些研究不仅涉及理论知识的深入，而且与实际应用紧密相扣。

机器人与相机转换基础

在机器人操作领域，线性矩阵被普遍用于描述机器人与相机之间的坐标转换。这一理论在多数情况下都适用，是坐标转换的根本。比如，在工业制造车间，工程师在搭建机器人视觉系统时，必须熟悉这一基础转换原理，以便进行精确的操作。而且，线性矩阵也是计算其他相关数据的参考。在研究机器人与相机互动时，深入理解这种关系非常重要。在众多工业应用中，机器人与相机的坐标转换在不同坐标系中都需要依据这一基础关系进行有效的数据交换。

在实际操作时，仅凭理论判断关联性是不够的，还需结合实际情况。以电子元件组装为例，机器人要对极细微的元件进行操作，这时，相机与机器人间的坐标转换必须极为精准，这样才能保证任务得以顺利进行。

坐标系讨论分情况

讨论内容包括了如何辨别相机和机器人，以及测量、校准和精度验证的方法。这一步骤非常关键且细致。在具体项目操作中，例如开发新的机器人视觉检测系统，我们会根据特定型号的机器人和相机的需求来操作。相机的类型有2D和3D之分，它们在机器人应用中对于坐标转换的要求不同。例如，3D相机可以直接测量棋盘格的角点和对应的三维坐标，而2D相机则不能。所以，在使用2D相机时，我们通常需要付出更多努力来处理数据，以便达到3D相机那样的效果。

观察机器人，它们的机械臂等部件各有特点，末端执行器的用途也有所区别。在将机器人坐标系转换成相机坐标系时，这些特点显得格外突出。所以，为了应对这些差异，我们使用的标定技术也各有不同。

Eye - to - hand问题求解

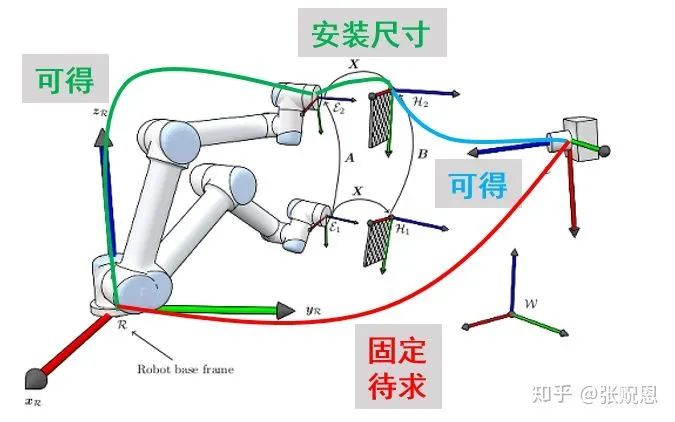
在处理eye-to-hand问题时，我们必须明确的是，相机与机器人基座坐标系间的转换矩阵是必须确定的。这一矩阵对机器人和相机的协同操作至关重要。以智能仓库的货物搬运机器人为例，相机固定在某点监控货物，机器人需根据相机提供的数据精确定位货物，以便搬运。这时，相机与机器人基座坐标系转换矩阵的精确性，将直接决定搬运作业的精确性。

找到解决方法的关键是识别棋盘格，并使用机器人的正向运动学。在标定阶段，棋盘格极为重要，必须将其固定在机器人末端。我们可以在相机坐标系中找到棋盘格角点的坐标，而机器人末端与基座之间的坐标则可以通过正向运动学来获得。掌握了这些信息，我们就能计算出转换矩阵。

坐标转换的实际操作

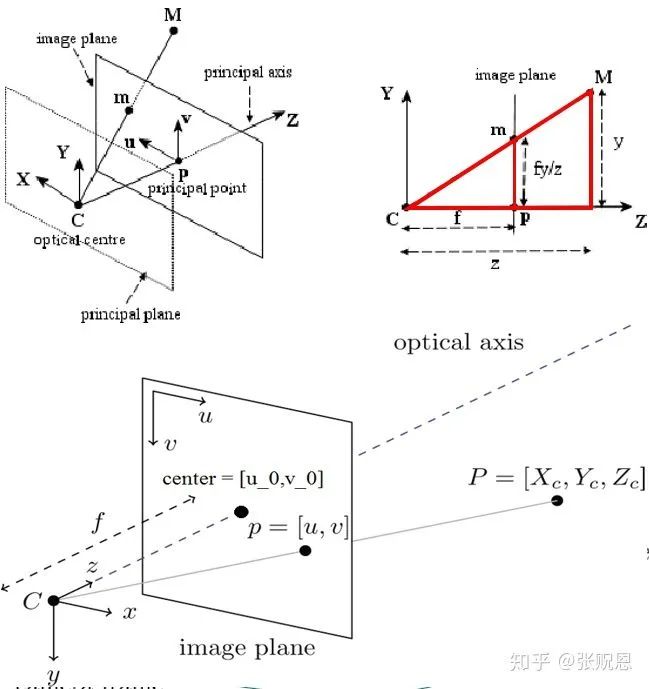
有一种技术能将平面图像上的坐标点转换成相机坐标系下的三维坐标。这项技术在机器人视觉领域需求很高。比如在汽车焊接的生产线上，机器人必须依据相机拍摄的图像来对汽车零件进行精确焊接。这就需要精确的坐标转换，而这又需要相机内参公式和深度信息的准确获取。要保证坐标转换的准确性，对内参公式等相关知识的深入理解和熟练运用极为关键。

存在一种技术，通过确定特定标记物的位置来计算目标点，例如在摄像头的视野四个角放置三个标记。该技术利用多个坐标系中标记物的坐标关系，确保坐标转换的精确度，其用途远超理论研究的范畴。

相机类型影响标定

2D相机和3D相机有明显的不同。2D相机不能直接得出物体的三维位置，一般用于视觉伺服控制，对机器人末端坐标的精度要求不高。而3D相机可以直接测量出棋盘格的角点和三维位置。比如，在艺术雕塑的3D扫描复制过程中，如果将3D相机装在可移动的机械臂上，就能准确获取各个点的位置信息。

因为2D相机有这个缺陷，所以在需要准确获得三维坐标的情况下，我们不得不采用间接测量方法。这样做无疑增加了操作的难度，还增加了出错的风险。

最直接的标定方式

要确定两个坐标系统，最直接的方式是测量同一组点在两个系统中的具体位置。举例来说，在研发医疗手术机器人时，这样做可以大大提高机器操作的精确性。我们一般使用矩阵的伪逆方法来计算坐标转换矩阵。这一步骤对数据的精确性要求非常高。因此，它对操作人员的数据采集准确性提出了严格的要求，哪怕是微小的误差，在矩阵计算后也可能引起较大的偏差。