科研人员和汽车行业的从业者都渴望对汽车实施精确操控,因此,打造一个既精确又实用的车辆数字模型显得尤为关键。这样的模型的好坏,将直接关系到车辆跟踪控制的效果。下面,我们将对车辆的运动学模型进行详细剖析。

模型构建意义
在车辆控制领域,建立运动学模型非常重要。汽车行业持续进步,无论是研发自动驾驶车辆,还是提高常规车辆的控制效能,都迫切需要这样一个精确的模型。精确描述车辆运动,对改善控制效果极为关键。所构建的模型不仅要真实反映车辆的实际状态,还要便于操作,这样才能更好地应用于实际。
运动学自行车模型结构
在自行车运动学的模型中,左右两个前轮被合并成了一轮,并以A点作为旋转的中心。后轮则经过等效处理,其旋转中心位于B点。转向的角度分别用δf和δr表示,这两个轮子都可以进行转向。如果系统中只有前轮可以进行转向,那么δr的值可以设定为0。车辆的重心位于C点,从A点和B点到重心的距离分别为lf和lr,而整个车辆的轴距L就是lf和lr两个距离的和。该模型通过四个状态参数来体现车辆此刻的行驶状况,这一模型既基础又至关重要。
车辆运动状态描述

车辆若以固定速度沿直线行驶,其动态可以通过X、Y和ψ三个坐标值来具体阐述。X和Y坐标的搭配能够精确指出车辆重心的具体位置,而ψ坐标则揭示了车辆行驶的方向。车辆重心的移动速度以V来表示,V与车辆纵向中心线形成的角度β,也就是车辆的侧向滑动角度。车辆行驶速度不快时,若速度向量V在A、B两点的方向和转向角度一致,这一条件对研究车辆动态极为关键。
瞬时旋转中心及转弯半径
O点是车辆旋转的轴心,AO线和BO线各自与车辆前后轮的旋转方向成直角,这两条线的交点就是O点。OC线的长度表示车辆行驶轨迹的半径R。车辆行驶速度较慢时,转弯半径的变化并不明显。此时,我们假设车辆偏航角的变化速度与车辆的角速度w相等。借助三角学的原理,我们成功推导出去除R的公式,随后据此建立了一个模型,该模型详细描述了自行车在惯性坐标系中的运动学特征。
常见车辆模型简化
多数汽车的后轮无法转向,因此在我们构建的单车模型中,我们假定后轮的转向角度为零,即δr为0。操控方向盘将直接导致前轮转向。在模型计算中,公式的变动部分可以简化。通常,车辆的后轴是固定的,若忽略前后轮的差异,我们可以通过特定的计算方法确定一个等效的转向角度。四轮汽车的模型和单车运动学模型建立了联系,只是对前轮转向角度进行了调整,将其改为两个前轮转向角度的平均值。
阿克曼转向几何规律
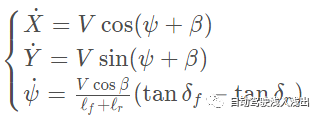

阿克曼将几何学的知识应用到了车辆转弯时内外转向轮轨迹不指向圆心的难题上。通过计算前内轮与前外轮的转角差,我们注意到一个有趣的现象:当车轮转向角度增加时,内外轮的转向角度差异也会相应增大。这一发现对于车辆的设计和转向控制至关重要,能够显著提升车辆的转向能力。
关于车辆运动学模型的发展趋势,您有何高见?若您觉得这篇文章写得相当不错,不妨点个赞,同时也可以将它转发出去,让更多人看到。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:http://www.mayuv.com/html/tiyuwenda/9812.html